Sep 21, 2015   [permalink]

On Being Late

It is your fault, but only sort of

Around the world, in businesses and governments, militaries and nonprofits, people wearily acknowledge that projects nearly always take longer and cost more than you expect. It's worst when you're doing something completely new (i.e., all the best and coolest projects of your career), but even if you're just turning the crank on a process that's been done many times, the real world has an uncanny habit of tossing sabots into the gears. Mathematician Douglas Hofstadter even codified this as Hofstadter's Law: "It always takes longer than you expect, even when you take into account Hofstadter's Law." Recursive snarkiness, ha ha.

As to the question of why things are late, people have been surprisingly incurious, or at least incapable of satisfying their curiosity. However, the work of Nassim Nicholas Taleb provides an important clue. In his 2007 book The Black Swan, Taleb asserts that "random" events actually fall into two categories: Gaussian randomness, where the outcomes fall along a neat, predictable bell curve, and power-law randomness, where there's actually no limit to how big an outcome you can see.

So: in a Gaussian water clock, each drop may have (for example) a 68% chance to land within a timing error of ± one-tenth of a second, a 4.4% chance of being off by more than two-tenths of a second, and only an 0.2% chance of being off by more than three tenths of a second. In a water clock governed by power-law statistics, the water drop may have that same 68% chance of being within 0.1 seconds of perfect, but a 4.4% chance of being off by 2.5 seconds, and an 0.2% chance of being off by 50 seconds. That's a huge difference, and Taleb's point is that if you blithely assume an event is going to be Gaussian when in fact it's power-law, then 68% of the time you'll never know the difference, and 28% of the time you'll say your models are pretty close, and 4% of the time you'll experience unpleasant, inexplicable anomalies, and 0.2% of the time you'll suffer an error of such cataclysmic proportions that no reasonable contingency plan could possibly absorb it. You are, in a word, fucked.

Applying this same logic to project timelines, we can treat completion as an event with an expected time of occurrence, and a certain random variance around that. The ETA is calculated quite simply, by breaking the task into subtasks, estimating how long each subtask will take (including which of them can happen concurrently and which ones have to be sequential), and then adding the times together. This process is especially clear, communicable, and defensible when laid out via Microsoft Project (or one of its many imitators) in the form of a Gantt chart.

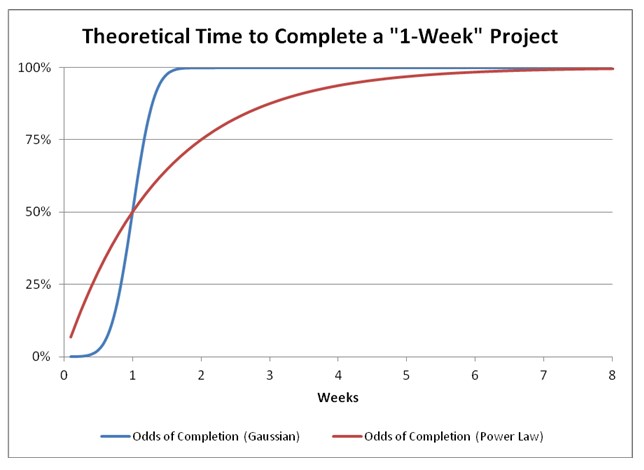
Unfortunately, this is just pretty bullshit, because it doesn't offer any insight into the possible variance around your ETA. The standard project management approach is to take the estimated time and double it, but this is (a) arbitrary, and (b) still very frequently not enough time. And here is where we can look to Taleb, because even if you know the standard deviation (and with enough experience, you can get pretty good at estimating it), the difference between a Gaussian and power-law completion date will still crush you. In the example below, both curves show a 50% chance of completion after 1 week of elapsed time.

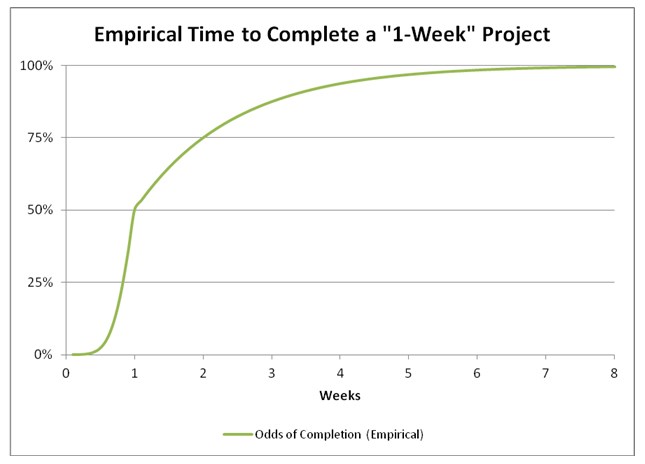
However, the power-law distribution shows a 25% chance of completion after just 3 days, which is clearly wrong if you've calculated your ETA correctly. The cumulative Gaussian curve shows virtually zero chance of this, which seems much more plausible. But the Gaussian curve also shows a 100% chance of completion by week 3, which also seems rather farfetched, whereas the power law shows a much more believable 88% chance. More importantly, the power law allows for the possibility that the project could drag on for four or five or even six weeks. Anyone who's ever worked on an engineering project knows that this really is possible, and occurs more frequently than we care to admit. So, in reality it seems the left side of our uncertainty curve is Gaussian, while the right side follows a power law.

Looking at this graph, it's fairly easy to pick out a confidence interval for completion of your project. If you're comfortable overrunning the deadline on a quarter of your projects, then doubling your estimate is fine. However, if you want a 90% on-time delivery rate, you should multiply the estimate by 3.3. See? Now you're a superstar project manager!

Even this picture is overly optimistic, though, because what happens if you break up the 1-week project into five 8-hour subprojects? A purely Gaussian or purely power-law curve would scale cleanly when subdivided this way, but because the two halves of our graph don't match, the stats are thrown into disarray, because each task has a 50% chance of being Gaussian and a 50% chance of tipping left into power-law territory. Thus, on average, we could expect one of our five subprojects to take 6.4 hours, one 7.2 hours, one 10.8 hours, one 18.4 hours, and one that takes a whopping 41.2 hours. Our one-week project now has a median completion time of 84 hours, or 2.1 standard work weeks!

But we could also subdivide the project into two subtasks, or ten, or a hundred, and each would distort the statistics in a slightly different way. Clearly, then, the actual median is the limit of this total as the number of subprojects approaches infinity (or the time for each subproject approaches zero). I'm way too lazy to work out the closed-form integral for something like this, but a quick numerical estimate tells me it's somewhere around 1.8 weeks. That's the median median.

Putting all this together, our 80% confidence interval for completion of a "1-week" project is actually 4.14 weeks. So if you report that you're a superstar who delivers on time, right? Oh, if only it were that easy! Because in fact, if you tell the business guys it's going to take four weeks for a task that seems like it should only take one, they'll fire your ass before you've even finished speaking.

Instead, you actually do just double your estimate, because that's standard business practice and you won't usually lose your job over doing the same wrong thing as everyone else. Then you can pad or fudge slightly, by saying "A little over two weeks, boss." And then you work your nerd ass off, packing 55 hours of work into each calendar week. That way, even when you're a little late on the delivery they can't really fault you for it, except to say "Jeez, Michael Bolton from Office Space, do a better job of predicting next time."

At which point you do not say, "You'd fire me if I did, asshole."

More anon.

[ comments | add a comment ]